Math Homework #3 Term-2 School Year 2009-10

Due date : Monday, December 7, 2009

Use model drawing to solve the story problem!

Frank and Rosa took a total of 7 minutes and 15 seconds to solve a math problem. If Rosa took 4 minutes and 5 seconds less than Frank, how long did Frank take to solve the problem?

Math Homework #2 Term-2 School Year 2009-10

Due date : Monday, November 30, 2009

Use model drawing method to solve this story problem!

Pedro purchased 5 shirts and 3 pairs of pants at the department store. All the shirts were the same price, and each pair of pants cost $1.20 more than each shirt. If Pedro spent $163.60 on all of the shirts and pants, how much did each shirt cost?

Math Homework #1 Term-2 School Year 2009-10

Click here for downloading worksheet of math homework about ABSOLUTE VALUE and GCF / LCM.

Due date : Monday, October 19, 2009

Math Project (Geometry)

•

• Make drawing of kinds of Polygon on a piece of A3 paper or carton paper as well as you can do, such as triangle (equilateral, isosceles, right), quadrilateral (rectangle, square, parallelogram, rhombus, kite), pentagon, hexagon, octagon, decagon, etc. as much as you can do. And put labels or explanation needed on it. You may make it full color.
• Submit it on Monday, September 7, 2009
• Your drawing will be your score in assessment report.

Math Homework #3 Term-1 School Year 2009-10

Due date : Monday, August 31, 2009

1. Open the website : http://www.shodor.org/interactivate/activities/
2. Choose / click on "Statistics" menu.
3. Explore this page on the website.
4. Make a summary based on your activities and learning.

Regards,
-Mr.Nuz-

Math Homework #2 Term-1 School Year 2009-2010

Due date : Tuesday, August 18, 2009

Dear students,

Click here to download the file. But if you want to get the hard-copy of the file, you may ask to math teacher in math class.

Best regards,
- Mr.Nuz -

Math Homework #1 Term-1 School Year 2009-10

Due date : Monday, August 10, 2009

Dear students,

For the first homework grade 6-7 cluster XYZ, download the file by click here.

Then print it and do it at home. Submit it on due date or earlier.

You also may submit it to my email : nuzeffendi@gmail.com but don't forget to write your name and subject title.

Best regards,
- Mr.Nuz-

Welcome to 6-7 XYZ

Dear Students,

Welcome back to new academic year 2009/2010 . . . :-)
My name is Mr. Nuz and I will be your math teacher for grade 6-7 cluster XYZ
I am happy to teach you math with fun . . . either you are !

Sincerely yours,
Mr. Nuz

Geometry and Measurement # 2

Please click here for downloading the worksheet about Geometry and Measurement.

Geometry and Measurement # 1

Learning and Practicing Geometry and Measurement, please click here.

Grade-7 Math Probability Project

During UAS-BN for grade-6, for daily math activities grade-7 is to make math probability project such as probability games and the rules of playing. The product should be colorful and attractive. The rules of playing can be fair or not-fair games.

Materials: You may use dices, playing cards, dominoes, spinners, etc.








If you have difficulty to find the idea, you may find it from internet or from the books. The project will be played together with grade-6 after UAS-BN end and grade-6 joints with grade-7 in math class.

Find the idea of this project! You may do this project together in math's class group.

Setup Al-Qur'an into MS-Word

When we are typing by using MS-Word (MS-Office), it is difficult to type Al-Qur'an and its tafseer.

Now Easy!

I want to share the software program that should be setup into MS-Word, just click this setup-quran-in-word-ind. After downloaded, extract the rar file then run exe file until installation process done. Then open MS-Word and you will see new icon "Al-Quran" menu on the top of MS-Word.

To be expert using this "Al-Quran" menu, try to explore it. . .

Semoga ALLOOH SWT memberikan Rahmat-Nya !

Math Magic Games

Situation :

Call your friends and tell them that you are able to read their mind. Ask them to think a number and don't let you know the number they are thinking. When they are counting you may act as a magician by closing your eyes and raising your hands to the sky.

Instruction :

"Think a number and don't let me know the number. Multiply the number with three, added by four, multiplied by two, divided by 2, added by two, divided by three and the last is subtracted by the number in your mind"

They will be surprise after you tell them that the the number their thought is "two".

Secret :

Whatever numbers they put in, the answer is always "two". Why? By using algebra equation!
If the number given is x, so we get the formula :

{[(2(3x+4)):2]+2}:3-x=2

The way :

If you want the answer is "three" just follow these steps:

(x+3)-x = 3

and put times 2 (or whatever number you want to put in) :
(2(x+3):2)-x=3

Expand the equation (2x+6):2-x=3
Change the equation to be [(2x+4)+2]:2-x=3

and put times 3 (or whatever number you want to put in) :
{[3(2x+4):3]+2}:2 - x = 3

And the last, expand the equation :
{[(6x+12):3]+2}:2 - x = 3

So, the instruction will be "Multiply the number you're thinking with 6, add 12, divided by 3, added by 2, divided by 2, and subtracted by the number"

And prove it if we put the number is 10 :
6 x 10 = 60
60 + 12 = 72
72 : 3 = 24
24 + 2 = 26
26 : 2 = 13
13 - 10 = 3

Have fun with math !!!

Congruent and Similar on Youtube

You may link these sites to learn "congruency and similarity" in math on Youtube.

resizing - stretching
congruent triangle activity
similar triangle-1
similar triangle-2
congruency & similarity
proportions & similarity
introduction to ratio
ratios and proportions-1
ratios and proportions-2

Math Project # 9 - Algebra

Algebra

Due date : Monday, February 9, 2009

1. If the difference of length and width of a rectangle is 2 cm and the perimeter of that rectangle is 52 cm, then determine the area of that rectangle!

2. If the sum of 8 consecutive odd numbers is 4000, then determine the odd numbers all!

Note:
You may submit the homework through email, but let me know by filling in the shoutbox (sidebar on the right)

Basic Geometric Forms

Basic Algebraic Properties

Algebraic Properties of Real Numbers

The basic algebraic properties of real numbers a,b and c are:

1. Closure: a + b and ab are real numbers
2. Commutative: a + b = b + a, ab = ba
3. Associative: (a+b) + c = a + (b+c), (ab)c = a(bc)
4. Distributive: (a+b) c = ac+ bc
5. Identity: a+0 = 0+a = a
6. Inverse: a + (-a) = 0, a(1/a) = 1
7. Cancellation: If a+x=a+y, then x=y
8. Zero-factor: a0 = 0a = 0
9. Negation: -(-a) = a, (-a)b= a(-b) = -(ab), (-a)(-b) = ab

Algebraic Combination

Factors with a common denominator can be expanded:



Fractions can be added by finding a common denominator:



Products of fractions can be carried out directly:



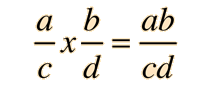
Quotients of fractions can be evaluated by inverting and multiplying:

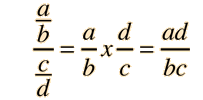
Parental Controls - Protect your children's computer !

Dear parents,

As parents sometimes we are too busy to monitor our children from the websites that is not appropriate for them to be watched. This is the software (free download) that you can install into your children computer or lap-top. This software is like a dog that always controls your children computer or laptop. When your children want to open the forbidden sites, the 'dog' will block the site.

Please follow the steps :

1. Click this website :

k9webprotection.com

2. Click "Download". You may choose which is suite to your computer operating system. Windows or Mac OS X
3. Click "Save"
4. Choose the file destination. For example "My Document"
5. Explore to "My Document" folder
6. Click "K9 - Web Protection" file
7. Click "Run"
8. Welcome to the Blue Coat ... --> click "Next"
9. Licence Agreement --> click "I agree"
10. K9 Release Note --> click "Next"
11. Choose Install Location --> click "Next"
12. Click "Get Licence"
13. Fill in the forms and use your (parents) private email address that your children are not able to open it, then finish this request by click "Request License".
Then leave it for a while...
14. Open your (parents) private email as mentioned point 13.
15. Copy the licence from K9 Web Protection Support by press Ctrl-C (for windows). And log out your (parents) private email.
16. Open again the window point 13 and paste the license you got from point 15. Then click "Next"
17. Creating Password (DONT'T LET YOUR CHILDREN KNOW THIS PASSWORD !!!) then click "Next". (You may change the password later)
18. Shortcut Placement --> click "Install"
19. Installation Complete --> click "Next"
20. Choose "Reboot Now" then click "Finish"
21. Wait for rebooting the computer and DONE.

If you (parents) want to open it, just click shortcut K9 Web Protection on the desktop, and now you (parents) are able to control your children's computer or lap-top.
Please learn the using of K9 Web Protection by reading GET HELP.
Don't forget to log out when you (parents) out from K9 Web Protection.

And now you will feel secure at all the time to leave your children exploring the internet . . . :-)

Best regards,
Mr.Nuz

Math Project # 8 - Algebra

Due date : Monday, February 2, 2009

1. Find the number described in each problem by writing and solving an equation
a) If Sarah substracts five times her number from 24, she gets 4. What is Sarah's number?
b) Twice Bill's number added to 17 is 7. What is Bill's number?
c) The sum of 4 times a number and 14 is 16. What is the number?
d) If Susan substracts 11 from one fourth of her number she gets 11. What is Susan's number?

2. The school drama club is performing its summer play at the community theatre. Props for the play cost $250, and the theatre is charging the drama club $1.25 for each ticket sold. So, the total cost, C, for the drama club to put on the play is C=1.25N+250, where N is the number of tickets sold. Customers pay $4 for each ticket, so the total amount collected from ticket sales is T=4N.
a) What is the cost if 213 tickets are sold?
b) How much are the total ticket sales if 213 tickets are sold?
c) What is the drama club's profit or loss if 213 tickets are sold?
d) If the total ticket sales are $780, how many people attended the play?
e) What is the cost of putting on the play for the number of people you found in d)?
f) How many tickets does the drama club need to sell to break even?
g) The drama club would like to earn a profit of $500 from play. How many tickets need to be sold for the club to meet this goal?

Free download math software (Geogebra)

Hi guys !

There is a math software and free download into your computer and you will be interesting to explore this math program.

Click this website :

geogebra.org

After open this website, click "Download GeoGebra" and follow next instruction. It's easy !

If you have problem to run this software because of there is no Java installed, you may download Java by click this website :

java.com

................................................................................................

How to use it? Just click HELP icon and read it . . .

Have a happy learn math . . . !!!

Regards,
Mr.Nuz

Algebra Practice

Terry has a walking rate 1 meter per second.
Jade has a walking rate 2 meters per second.
Jerome has a walking rate 2.5 meters per second.

1. If Terry, Jade, and Jerome leave school together and walk toward the frozen yogurt shop at the rates given, how far apart will they be after 1 minute?

2. If the yogurt shop is 750 meters from school, how long will it takes each student to walk there?

3. When Jerome arrives at the yogurt shop, how far away will Terry be?

4. Make a table showing the distance walked by each student after different numbers of seconds. How does the walking rate affect the data in the table?

5. Graph the time and distance data for the three students on the same coordinate axes. How does the walking rate affect the graphs?

6. For each student, write an equation that gives the relationship between the time and the distance walked. Let "d" represent the distance in meters and "t" represent the time in seconds. How does the walking rate affect the equations?

How to teach algebra to the children (part 2)

In this experiment, you will do an experiment to test some of the principles involved in building bridges.

Equipment : several A4 of paper, two books of the same thickness, a small plastic cup, and about 50 pennies.

Directions :
1. Make a paper "bridge" by folding up 2 cm on the each long side of one of the paper strips.
2. Suspend the bridge between the two books. The bridge should be overlap each book by about 1 cm. Place the plastic cup in the center of the bridge.
3. Put pennies into the cup, one at a time, until the bridge crumples. Record the number of pennies you added to the cup. This number is the "breaking weight" of the bridge.
4. Put two strips together to make a bridge of double thickness. Find the breaking weight for this bridge. Repeat this experiment to find breaking weight for bridges made from three, four, and five strips of paper.

Questions :
Before answering the questions, you have to make a table and draw a straight line on a grid paper that seems to fit the pattern in the (thickness - on the horizontal axes, breaking weight - on the vertical exes) data you graphed.
1. Based on your graph model, what breaking weights would you predict for bridges 6 layers thick and 7 layers thick?
2. Suppose you could use half-layers of paper to build the bridges. What breaking weights would you predict for bridges 2.5 layers thick and 3.5 layers thick?
3. Could you make an equation that related between layers thick (x) and breaking weight (y), which is the equation would be y = mx + c ? Where : m is the slope or gradient and c is constant or y-intercept on the graph.

How to teach algebra to the children (part 1)

In this experiment, you will investigate how the height from which a ball is dropped is related to the height it bounces.

Equipment : a meterstick and a ball that bounces.

Directions :
1. Make a table with columns for recording drop height and bounce height.
2. Hold the meterstick perpendicular to a flat surface, such as an uncarpeted floor, table, or a desk.
3. Choose and record a height on the meterstick as the height from which you will drop the ball. Hold the ball at this height.
4. Drop the ball, and record the height of the first bounce. (You may have to do this several times before you feel confident you can make a good estimate of the bounce height).
5. Repeat this for several different drop heights.

Questions :
Before answering the questions, you have to make a coordinate graph of data you collected.
1. What variables did you investigate in this experiment? Describe the relationship between the variables.
2. Predict the bounce height for a drop height of 2 meters. Explain how you made your prediction.
3. Predict the drop height needed for a bounce height of 2 meters. Explain how you made your prediction.
4. What bounce height would you expect for a drop height of 0 (zero) centimeters? Where would this be on the graph?
5. Could you make an equation that related between drop height (x) and bounce height (y), which is the equation would be y = mx + c ? Where : m is the slope or gradient and c is constant or y-intercept on the graph.

Math Project # 7 - Algebra

Henri has been walking every day and has increased his speed. He now walks at a rate of 2 meters per second. Emile has not been practicing but finds that he can still walk at a rate of 2.5 meters per second. Emile and Henri decide to have another race. Emile gives his brother a head start of 40 meters.

1. Write an equation for each brother that shows the relationship between distance walked and time.

Direction : Use graphs, tables, or your equations to answer questions 2-4. In each question, sketch the section of graph (with the sclae marked) or the table and indicate where you found the answers, or record the computational work you do.

2. Find each brother's distance at 60 seconds.

3. Find the time when Emile catches up with his brother.

4. What are the y-intercepts? Explain how you can find the y-intercepts in each representation-table, graph, and equation.

Math Project # 6 - Algebra

1. Find one example of relationship data of two variables (can be in short story / problem, can be in form of table or graph or chart)

2. Predict what will happen or how much is the y-axis value if you increase the x-axis value until 10 units.